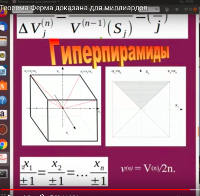
Необычайная красота и лаконичность формулировки Великой теоремы Ферма заставляют искать её наглядное  решение. Такое решение нашёл россиянин Марат Авдыев 04 февраля 2020 г. с помощью представления уравнения aⁿ + bⁿ = cⁿ в виде трёх вложенных друг в друга гиперкубов, при этом  центр каждого из них совпадает с началом координат n -мерного пространства. Оказалось, что в целых числах такая фигура в виде сочетания 3-х кубов не может иметь свойство симметричности в изотропном пространстве. Кубы подобны др. другу, но один из них всегда будет иметь иррациональное ребро. Кто виноват в утрате симметрии фигуры? 

Скептики продолжают считать, что Пьер де Ферма, вероятнее всего, заблуждался. Между тем, последовательное применение основных принципов физики, геометрии, лабораторных испытаний заставляют думать иначе.

Этого не может быть никогда!

Первая реакция - шок на очередной фейк. Вот если бы доказал маститый остепененный учёный и желательно с образованием из Гарвардского университета или иного из Лиги Плюща - тогда всё было бы в порядке! А иначе: не верим и не будем даже читать, чтоы не утомлять глаза и не напрягать мозги. Не может доказать россинин из глубинки Велику Теорему! Это вероятно, очередной параноик!

Ну что ж всё новое воспринимается серьезными людьми примерно так. За почти четыре века сложилась именно такая научная парадигма: Ферма сильно преувеличил свои достижения, проще говоря обманул доверчивую публику, и тысячи попыток «звёзд от математики» это доказывает. Даже Энрю Уайлс, теперь знаменитый профессор математики из Принстонского университета* потратил около полутора сотен страниц на поиск Истины! - Иного решения нет.

Чёрный лебедь является неожиданно

По наблюдению Насима Николаса Талеба, долгое отсутствие некого редчайшего события еще не доказывает что оно невозможно. Чёрный лебедь является неожиданно. В математике произошло то же самое, а может быть всё просто потому, что за теорем взялся физик :-)

Суммируя сказанное, приходим к выводу, что уравнение Теоремы Ферма, эквивалентное:

cⁿ - bⁿ = aⁿ 
не имеет решения для случая n > 2 в Iⁿ из-за конфликта размерности, симметричности, нарушения непрерывного следования слоёв. В левой части множество Si слоёв  (n-1) размерности. В правой — гиперкуб n- размерности Слева фигура, соответствующая выражению, асимметрична, но справа — симметрична. Следовательно не все элементы тройки чисел {a, b, c} ∈ к Iⁿ , хотя бы один из них является иррациональным, т. е. в общем случае {a, b, c} ∈ Rn, и нет такой тройки чисел, которые помогут восстановить нарушенную симметрию гиперкубов — необходимого условия (7), как необходимого условия для

*

Скептики продолжают считать, что Пьер де Ферма, вероятнее всего, заблуждался. Между тем, последовательное применение основных принципов физики, геометрии, лабораторных измерений заставляют думать иначе.

Теорема Ферма может быть доказана в одном рисунке и в одной формуле. Выпишем формулу (3) в развернутой форме, она может насчитывать натуральное число слоёв i. Это может быть достаточно длинная, но простая для понимания формула, силу V₁⁽ⁿ⁾= V₃⁽ⁿ⁾:

1ⁿ+ V⁽ⁿ⁾{S₁,S₂ ,S₃, S₄ . . S_k} = V⁽ⁿ⁾{S_k+l+1,S_k+l+2. . .S_k+l+m}.

Из этого выражения с учётом геометрии слоёв следует, что требования непрерывности, последовательности  слоёв, симметричности фигуры и равенства  объёмов V1⁽ⁿ⁾ = V3⁽ⁿ⁾ являются взаимоисключающими при n > 2 в силу изоморфизма каждого из только что перечисленных слоёв Si фигуре, имеющей неустранимый дефект S1 =  2ⁿ — 1,  что легко понять из геометрииС этих позиций Великая теорема Ферма доказывается тщательным рассмотрением всего лишь одним взглядом, как в древних Индийских трактатах по математике, где доказательство в одном рисунке сопровождалось только одним словом: Смотри!

Для понимания всех обозначений этой формулы можно прочесть пубилкацию ** целиком.  

Но люди, занимающие высокие посты в науки, настолько заняты проведением совещаний, что им некогда вникать в суть теоремы. Даже на 13 страницах.  

Так что доказательство ждёт своего часа, когда облеченные властью и занимающие высокие должности учёные, найдут время уделить внимание доказательству. Не просто решается вопрос с регистрацией открытий в России: Российская Академия Естественных наук даже не разместила реестра научных открытий на своем сайте. Такой реестр есть в Википедии, но по состоянию на 25 лет назад. Пора бы заметить очевидные перемены в обществе.

  И всё- таки мы надеемся на то, что Теорема Ферма рано или поздно станет частью школьной программы, наряду с теоремой Пифагора, хотя, конечно она требует определенной помощи со стороны педагога - математика. 

 * При́нстонский университет — частный исследовательский университет, один из старейших и известнейших университетов в США. Находится в городе Принстон, штат Нью-Джерси. Университет является одним из восьми университетов Лиги плюща и одним из девяти колониальных колледжей, основанных до Американской революции

 **  ТЕОРЕМА ФЕРМА С ПОЗИЦИИ ФИЗИКИ В ШКОЛЕ Принято к публикации 07 февраля 2020 Научным издательством «Зебра», дата выхода коллективной монографии - апрель 2020 г.

Ссылки на литературу и др. источники
1. В. Серпинский. Пифагоровы треугольники. — М.: Учпедгиз, 1959. — 111 с.
2. D. E. Joyce. Euclid's Elements. — Clark University, June 1997. — С. Book X, Proposition XXIX.
3. Douglas W. Mitchell. An Alternative Characterisation of All Primitive Pythagorean Triples // The Mathematical Gazette. — July 2001. — Т. 85, вып. 503. — С. 273–5.
4. Wiles's proof of Fermat's Last Theorem ref. https://en.wikipedia.org/wiki/Wiles
%27s_proof_of_Fermat%27s_Last_Theorem#cite_ref-Singh_1-0 last visit 25.01.2020
5. Г.Л.Коткин, В.Г.Сербо. Аналитическая механика: Дополнительные вопросы. Учеб. пособив /Новосиб.ун-т. Новосибирск, 1987. 84 с.
6. Бухгольц Н. Н. Основной курс теоретической механики. Ч. 1. 10-е изд. — Спб.: Лань, 2009. — 480 с. — ISBN 978-5-8114-0926-6.